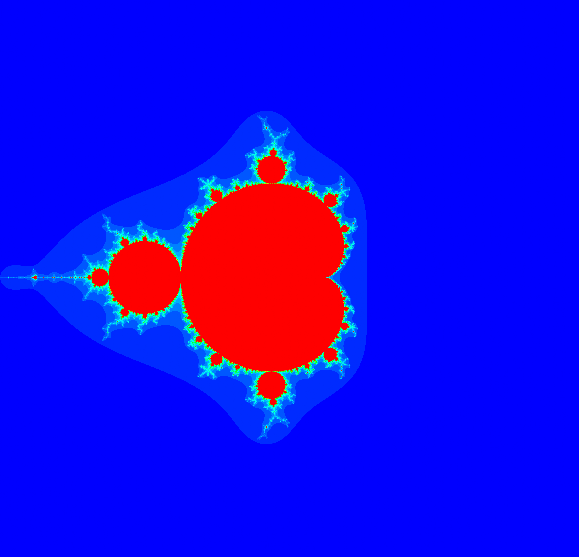
Plotting and computing area of Mandlebrot Set using OpenMP and MPI

The Mandelbrot set, named after Benoit Mandelbrot, is a fractal. Wikipedia defines it as the set of complex numbers c for which the function $f_c(z) = z^2 + c$ does not diverge when iterated from $z=0$, i.e., for which the sequence $f_c(0)$, $f_c(f_c(0))$, etc., remains bounded in absolute value. The target of this project was to compute the area of Mandlebrot Set and plot it at a high resolution using parallel computing techniques OpenMP and MPI. For OpenMP, the speedup was compared for different scheduling techniques and Amdahl’s Law. For MPI, the speed up was compared between weak and strong scaling. The MPI code was developed for two cases: domain equally partitioned between processes and by partitioning the domain into two groups of processes by creating a new communicator.