Solution to Laplace Equation using Preconditioned Conjugate Gradient Method with Compressed Row Storage and MPI

Laplace’s equation is the simplest example of elliptic partial differential equations. The general theory of solutions to Laplace’s equation is known as potential theory. The solutions of Laplace’s equation are the harmonic functions, which are important in many fields of science, notably the fields of electromagnetism, astronomy, and fluid dynamics, because they can be used to accurately describe the behavior of electric, gravitational, and fluid potentials. In the study of heat conduction, the Laplace equation is the steady-state heat equation. [Wiki]

In this project, a linear system of equations ($AX=B$) was formed that will give direct solution at each grid point for the laplace equation. A conjugate gradient krylov solver was then built to solve the system of equations iteratively. Jacobi preconditioning was employed to speedup the solver. Owing to the large problem size, compressed row storage was used to store A matrix in the linear system of equations thus generated.

The code was parallelized using MPI. The domain and the matrix storage was decomposed into well balanced chunks and assembled locally. The accuracy of solution, performance and scalability of this code was also studied.

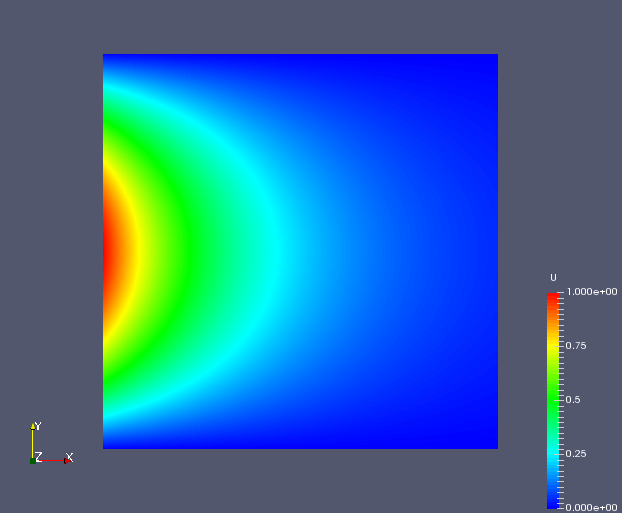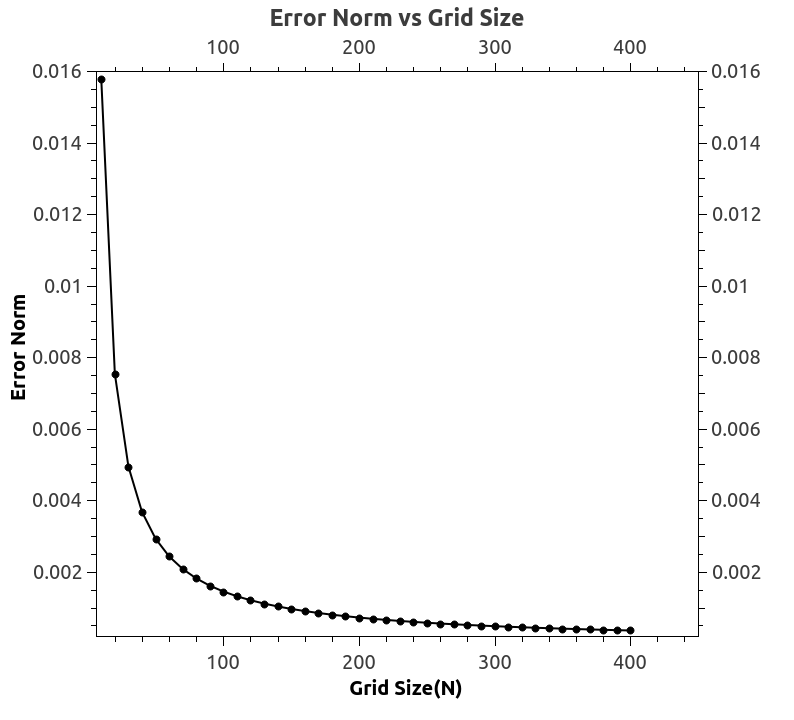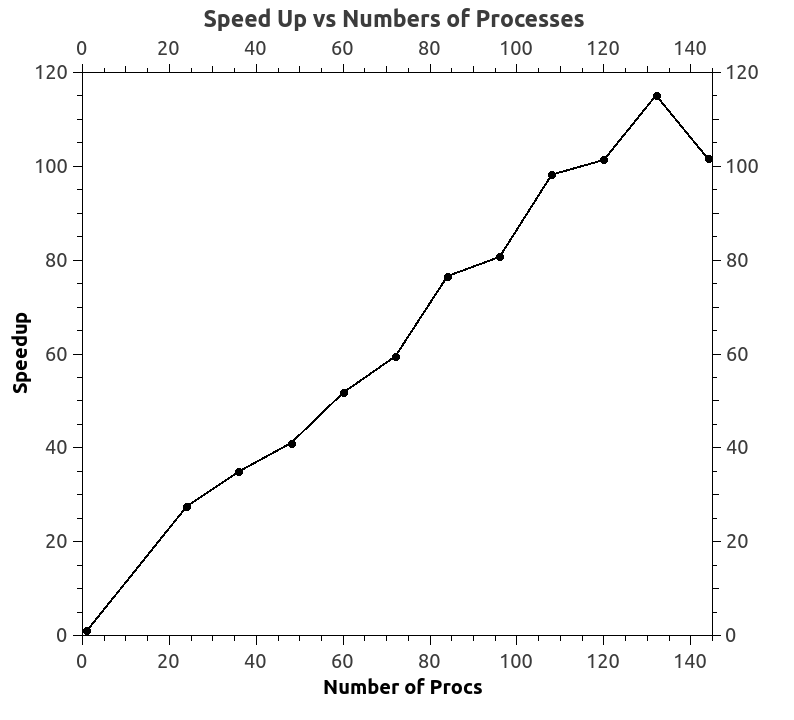Error Norm	Speedup